Para quienes no tiene acceso a Internet o medios tecnológicos en el siguiente enlace pueden descargar la version imprimible para estudiar --> AQUI
INTRODUCCIÓN
INTRODUCCIÓN
Observa detenidamente la animación.
Fuente: https://contenidosparaaprender.colombiaaprende.edu.co/
Ahora indica en tu cuaderno un aspecto importante que hayas notado sobre los logaritmos y su historia.
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ESTOS SON LOS OBJETIVOS PARA ESTA SEMANA
Reconocer la función logarítmica a partir de modelos utilizados en contextos de las ciencias naturales.
- Interpretar expresiones algebraicas que tienen logaritmos y representan situaciones de variación.
- Interpretar situaciones de variación identificando relaciones de tipo funcional logarítmicas.
- Establecer estrategias para representar funciones logarítmicas que caracterizan situaciones de variación.
AHORA VAMOS CON LA ACTIVIDAD 1.
A continuación encontrarás diferentes situaciones, léelas y escribe cómo las resolverías.
SITUACIÓN 1. La intensidad de un terremoto típicamente se mide entre 2 y 10 en la escala de Richter. Cualquier terremoto que se registra por debajo de 5 es un terremoto menor; pueden mover un poco el suelo, pero normalmente no son lo suficientemente fuertes para causar algún daño. Los terremotos que miden entre 5 y 7.9 en la escala de Richter son mucho más severos y cualquier terremoto por encima de 8 causará mucho daño. ( El grado más alto jamás registrado para un terremoto fue de 9.5, durante el terremoto de 1960 en Valdivia, Chile.). Un terremoto mide una amplitud de 392 veces más grande que la Amplitud mas pequeña "Ao". ¿Cuál es la magnitud de este terremoto usando la escala Richter, en décimas? Escribe tu respuesta.
SOLUCIÓN.
Usa la ecuación de la escala Richter.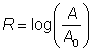
SOLUCIÓN.
Usa la ecuación de la escala Richter.
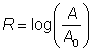
Como A es 392 veces más grande que A0, A = 392A0. Sustituye esta expresión por A. resuelve, utiliza la calculadora para hallar el logaritmo y expresa con décimas.
SITUACIÓN 2. El sonido se mide en una escala logarítmica usando una unidad que se llama decibel. La fórmula se parece mucho a la de escala de Richter.
donde P es la potencia o intensidad del sonido y Po es el sonido más débil que puede captar el humano. Una bomba de agua caliente tiene un índice de ruido de 50 decibeles. Una lavadora de platos, tiene un índice de ruido de 62 decibeles. ¿Qué tan intenso es el ruido de la lavadora comparado con el ruido de la bomba?. Escribe tu respuesta.
SITUACIÓN 3. La medida de acidez de un líquido se llama pH del líquido. Está basada en la cantidad de iones de hidrógeno (H+) en el líquido. La fórmula del pH es:
donde [H+] es la concentración de iones de hidrógeno, dada en una unidad llamada mol/L (“moles por litro”; un mol es 6.022 x 1023 moléculas o átomos). Líquidos con pH bajo (hasta 0) son más ácidos que los que tienen un pH alto. El agua, que es neutral (ni ácida ni alcalina) tiene un pH de 7.0. Si el jugo de limón tiene un pH de 1.7, ¿cuál es la concentración de iones de hidrógeno (in mol/L) en el jugo de limón, en centésimas?.
Con la ayuda de tus amigos, familia y/o consulta en Internet resuelve los siguientes ejercicios:
La función logarítmica
a. Observa las siguientes gráficas que representan funciones logarítmicas y analiza el crecimiento o decrecimiento de cada una y si la función es negativa o positiva.
b. Responde las siguientes preguntas:
¿Qué números conforman el dominio y qué números conforman el rango?
¿En qué partes son continuas?
¿Qué sucede cuando a es mayor que 1?
¿Qué sucede cuando a es menor que 1?
¿Por qué puntos pasan siempre las gráficas que observaron?
AHORA VAMOS CON LA ACTIVIDAD 3.
Representando la función logarítmica
a. El plano cartesiano representa los datos presentados en la tablas y escribe la expresión algebraica para la función.
RESUMEN














y el plan de apoyo también tenemos que realizarlo todos?
ResponderBorrarHola, el plan de apoyo es para todos, especialmente aquellos estudiantes que estan bajos de calificaciones y no olviden hacer la autoevaluacion, para tener la totalidad de notas del primer periodo
BorrarProfe la primera situación esta mal, La escala de ritchter se utiliza hasta una magnitud máxima de 6,9; entonces no se puede utilizar la formula M = log A + xlog(xΔt), o no seria precisa para resolver la primera ecuación.
ResponderBorrarNo es que esté mal, lo que pasa es que La sismología mundial usa esta escala Ritcher para determinar las fuerzas de sismos de una magnitud entre 2,0 y 6,9. Mientra los sismos con magnitud superior a 6,9 se miden con la escala sismológica conocida como "magnitud de momento", que es una ecuación que discrimina mejor (valores extremos).
BorrarSi se habla de la escala de Ritcher es por que la magnitud del terremoto mencionado en la situación 1, debe estar entre 2 y 6,9, y el ejercicio lo que solicita es precisamente eso, cuál es la magnitud del terremoto si este presenta una amplitud de 392 veces más grande que la Amplitud mas pequeña "Ao".
De acuerdo a lo anterior, lo que se quiere es que ud manipule la ecuación dada en el ejercicio que involucra logaritmos y con los datos conocidos intente hallar la magnitud del terremoto.
BorrarPara cuando es el trabajo puesto mediante esta página web?
ResponderBorrarLa idea es esta semana hasta el 24 de abril hay que trabajar en ello y enviarme los resultados del trabajo que realizaron en el cuaderno.
BorrarLes recuerdo que en este en lace de Skype, estaré en linea resolviendo dudas y haciendo trabajo pedagógico. https://join.skype.com/zrdNXUE5q9k1
Autoevaluación 4 soy kevin perez
ResponderBorrarHola Kevin, para llevar un mejor control, en la pestaña de autoevaluacion hay un link para llenar un formulario con sus datos e ingresa el resultado de su valoración,
Borrar